京都大学基础物理学研究所博士课程学生白川雄贵、该研究所森前智行副教授以及NTT社会信息研究所上席特别研究员(京都大学基础物理学研究所特任副教授)山川高志的研究团队,从密码理论这一新视角证明了量子计算机比传统计算机更快的“量子优越性”的必要充分条件。该研究成果已于6月27日在理论计算机科学国际会议“STOC 2025”上发表。
(供图:京都大学)
人们期待量子计算机能快速解决传统计算机需耗费大量计算时间的难题(量子优越性),但这种优越性并非始终存在。
研究团队认为,要理解量子计算机性能并发挥其能力,必须明确回答“在何种条件下存在量子优越性”及“实现量子优越性需要什么”等问题。
在数学上,当命题“A则B”与其逆命题“B则A”同时成立时,我们说A与B互为必要充分条件。要证明量子计算机的优越性,就必须满足这种必要充分条件。
迄今为止,例如针对采样问题、搜索问题等需要解决的问题,提出了量子优越性定义,并在特定条件下证明了其存在。但这些仅是充分条件,是否真正构成必要条件一直未被明确理解。
因此,此次研究为夯实量子优越性的理论基础,着手解决“量子优越性的必要充分条件是什么”这一根本问题。具体而言,团队研究了近年量子密码领域提出的“单向性谜题”这一密码功能的安全性与量子优越性存在的关系,并从数学上证明了二者等价。
这种密码是量子计算机生成的、传统计算机无法破解的谜题。此外,等价性意味着如果密码功能安全,则可构建展示量子优越性的任务,如果存在量子优越性,则可构造出安全的密码功能。
此次成果通过整合量子计算理论与密码理论各自发展的技术和思路,提出连接“量子优越性”与“密码安全性”这两个看似无关概念的新框架而得以实现。
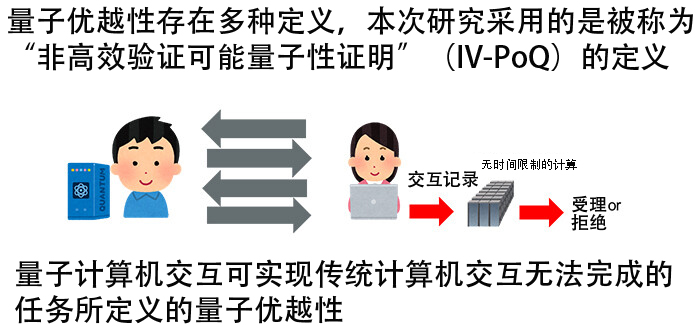
研究团队特别关注了“非高效验证可能量子性证明(IV-PoQ:Inefficient-Verifier Proofs of Quantumness)”这一交互式协议。该协议使不具备量子计算机的验证者与拥有量子计算机的证明者交互,从而验证对方是否真的具备量子计算能力。
研究从数学上证明了该协议存在的必要充分条件与“单向性谜题”这一密码功能的安全性一致,从理论上揭示了量子优越性与密码安全性具有等价关系。
研究团队指出,此次成果的意义不仅在于明确了量子优越性的必要充分条件,还在于量子计算理论与密码理论间存在的这种关联性有望对两个领域产生相互影响。
其意义之一在于,未来量子优越性的实证实验与理论研究将在更坚实的密码理论基础上推进。之二是这一成果意味着“如果量子优越性不存在,则当前多数被视为安全的密码功能将面临安全性崩塌”。
这种安全性崩塌风险不仅涉及量子密码,更将波及当前广泛使用的传统计算机密码及亟待普及的抗量子计算机密码,对信息安全领域具有重大启示意义。
原文:《科学新闻》
翻译:JST客观日本编辑部
【论文信息】
期刊:Proceedings of the 57th Annual ACM Symposium on Theory of Computing
论文:Cryptographic Characterization of Quantum Advantage
DOI:10.1145/3717823.3718133













